Question

Worker A works at a constant rate and, working alone, can complete a job in 6 hours. Worker B works at a constant rate and, working alone, can complete the same job in 5 hours. Worker C works at a constant rate and, working alone, can complete the same job in 3 hours.

Answer 1

`R= (1job)/(1.429 hours)`

So then we will have that the 3 working together will complete 1 job in approximately 1.429 hours for this case.

Step-by-step explanation:

If we want to express the situation in math terms and find the number of hours that takes to complete 1 job with the 3 at the same time, we can do this.

For this case we have the following rates:

`R_A =(1job)/(6hours)`

`R_B =(1 job)/(5 hours)`

`R_C=(1job)/(3 hours)`

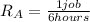
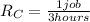
And we know that working together the rate would be the addition of the rates like this:

`R=R_A +R_B +R_C = (1job)/(6hours)+(1job)/(5hours)+(1job)/(3hours) =(7 jobs)/(10hours)`

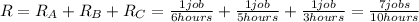
And if we divide the numerator and denominator by 7 we got:

`R= (1job)/(1.429 hours)`

So then we will have that the 3 working together will complete 1 job in approximately 1.429 hours for this case.