Question

You have to decide between two different companies that sell dirt. Company A sells dirt for $137.5 for 50 square feet and has a delivery fee of $100 dollars. Company B sells dirt for $15 for 5 square feet and offers free delivery. How much dirt do you need to buy for both companies to charge the same.

Answer 1

You need to buy 400 square feet of dirt for both companies to charge the same

Solution:

Given that,

Company A sells dirt for $137.5 for 50 square feet and has a delivery fee of $100 dollars

Dirt sold for $137.5 for 50 square feet

Let us find dirt sold for 1 square feet:

50 square feet = $ 137.5

1 square feet =
`(137.5)/(50) = 2.75`

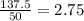
Thus dirt sold for $2.75 for 1 square feet

Company A has a delivery fee of $ 100 dollars

Amount Charged by company A:

Let "x" be the amount of dirt bought for 1 square feet

A = 2.75(x) + 100

A = 2.75x + 100 --- eqn 1

Company B sells dirt for $15 for 5 square feet and offers free delivery

Dirt sold for $ 15 for 5 square feet

5 square feet = $ 15

1 square feet =
`(15)/(5) = 3`

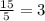
Thus dirt sold for $ 3 for 1 square feet

Company B offers free delivery

Amount Charged by company B:

A = 3x ---- eqn 2

Let us equate eqn 1 and eqn 2 to find the dirt you need to buy for both companies to charge the same

2.75x + 100 = 3x

3x - 2.75x = 100

0.25x = 100

x = 400

Thus you need to buy 400 square feet of dirt for both companies to charge the same