Question

for every natural number n, n^5 + 4n is a multiple of 5 could begin with... what is the appropriate next step

Answer 1

Answer: The proof is done below.

Step-by-step explanation: We are given to prove that the following statement is true :

"For every natural number n,
`n^5+4n` is a multiple of 5."

We will prove the above statement by MATHEMATICAL INDUCTION.

Let n = 1. Then, we get

`n^5+4n=1^5+4*5=5,` a multiple of 5.

Let n = 2. Then, we get

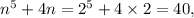`n^5+4n=2^5+4*2=40,` a multiple of 5.

Let the statement be true for n = m, where m is a natural number.

So,

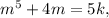`m^5+4m=5k,` for any natural number k.

Then,

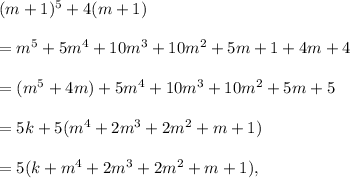`(m+1)^5+4(m+1)\\\\=m^5+5m^4+10m^3+10m^2+5m+1+4m+4\\\\=(m^5+4m)+5m^4+10m^3+10m^2+5m+5\\\\=5k+5(m^4+2m^3+2m^2+m+1)\\\\=5(k+m^4+2m^3+2m^2+m+1),` which is a multiple of 5.

Therefore, if the statement is true for n = m, then it is true for n = m+1.

That is, the statement is true for all natural numbers n.

Hence proved.