Question

Which product will result in a sum or difference of cubes? (x + 7)(x2 – 7x + 14) (x + 8)(x2 + 8x + 64) (x – 9)(x2 + 9x + 81) (x – 10)(x2 – 10x + 100)

Answer 1

C

Explanation:

Answer 2

Option 3)

`x^3-9^3 = (x-9)(x^2 + 9x + 81)`

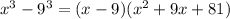
Explanation:

We use the identities:

`a^3 + b^3 = (a+b)(a^2-ab+b^2)\\a^3-b^3 = (a-b)(a^2+ab+b^2)`

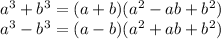
1.

`(x + 7)(x^2 -7x + 14)`

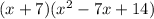
It is not a sum or difference of cubes because it does not satisfies the identity.

2.

`(x + 8)(x^2 + 8x + 64)`

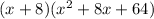
It is not a sum or difference of cubes because it does not satisfies the identity.

3.

`(x - 9)(x^2 + 9x + 81)\\\text{Comparing with the identity:} \\a^3-b^3 = (a-b)(a^2+ab+b^2)\\\text{We get}\\a = x\\b = 9\\x^3-9^3 = (x-9)(x^2 + 9x + 81)`

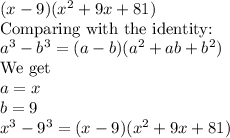
Thus, it can be expressed as a difference of cubes.

4.

`(x - 10)(x^2 - 10x + 100)`

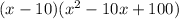
It is not a sum or difference of cubes because it does not satisfies the identity.