Answer:
Option 3)
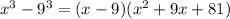
Explanation:
We use the identities:
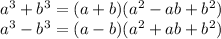
1.
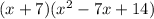
It is not a sum or difference of cubes because it does not satisfies the identity.
2.
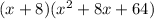
It is not a sum or difference of cubes because it does not satisfies the identity.
3.
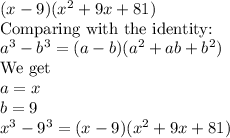
Thus, it can be expressed as a difference of cubes.
4.
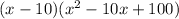
It is not a sum or difference of cubes because it does not satisfies the identity.