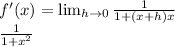Question

Differentiation by first principal

Answer 1

1 / (1 + x²)

Explanation:

Derivative of a function by first principle is:

`f'(x)= \lim_(h \to 0) (f(x+h)-f(x))/(h)`

Here, f(x) = tan⁻¹ x.

`f'(x)= \lim_(h \to 0) (tan^(-1)(x+h)-tan^(-1)x)/(h)`

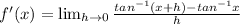
Use the difference of arctangents formula:

`tan^(-1)a-tan^(-1)b=tan^(-1)((a-b)/(1+ab))`

`f'(x)= \lim_(h \to 0) (tan^(-1)((x+h-x)/(1+(x+h)x) ))/(h)\\f'(x)= \lim_(h \to 0) (tan^(-1)((h)/(1+(x+h)x) ))/(h)`

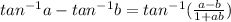
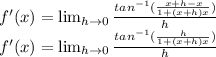
Next, we're going to use a trick by multiplying and dividing by 1+(x+h)x.

`f'(x)= \lim_(h \to 0) (tan^(-1)((h)/(1+(x+h)x) ))/(h)(1+(x+h)x)/(1+(x+h)x) \\f'(x)= \lim_(h \to 0) (1)/(1+(x+h)x) (tan^(-1)((h)/(1+(x+h)x) ))/((h)/(1+(x+h)x))`

We can now evaluate the limit. We'll need to use the identity:

`\lim_(x \to 0) (tan^(-1)x)/(x) =1`

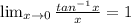
This can be shown using squeeze theorem.

The result is:

`f'(x)= \lim_(h \to 0) (1)/(1+(x+h)x)\\(1)/(1+x^2)`