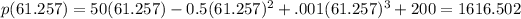Answer:
The level of wages that maximize tge profit is $61.257
And the correspond value for the profit is:
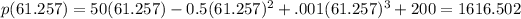
Step-by-step explanation:
For this case we have the following function:
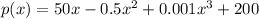
Where x represent the daily wages paid
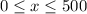 , and p(x) the profit, the objective is maximize this function, and in order to do this the first step is derivate the function respect to x and we got this:
, and p(x) the profit, the objective is maximize this function, and in order to do this the first step is derivate the function respect to x and we got this:
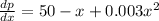
As we can see we have a quadratic equation now we need to set up equal the derivate obtained to 0 and then solve for the critical points, like this:
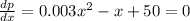
We can use the quadratic formula given by:
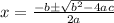
And for this case a=0.003 , b=-1 , c =50
Replacing this we got :
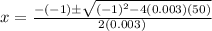
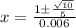
And we got:
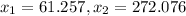
Now we need to find the second derivate, like this:
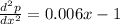
And we can replace the values obtained:

So then 61.257 is a maximum.
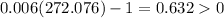
So then 272.076 is a minimum.
So then the level of wages that maximize tge profit is $61.257
And the correspond value for the profit is: