Question

[6.18] ([1] 7.52) Resistors to be used in a circuit have average resistance 200 ohms and standard deviation 10 ohms. Suppose 25 of these resistors are randomly selected to be used in a circuit. a) What is the probability that the average resistance for the 25 resistors is between 199 and 202 ohms? b) Find the probability that the total resistance does not exceed 5100 ohms.

Answer 1

Answer: a) 0.5328 b) 0.9772

Explanation:

Given : Resistors to be used in a circuit have average resistance 200 ohms and standard deviation 10 ohms.

`\mu=200` and
`\sigma=10`

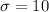
We assume that the resistance in circuits are normally distributed.

a) Let x denotes the average resistance of the circuit.

Sample size : n= 25

Then, the probability that the average resistance for the 25 resistors is between 199 and 202 ohms :-

`P(199<x<200)=P((199-200)/((10)/(√(25)))<(x-\mu)/((\sigma)/(√(n)))<(202-200)/((10)/(√(25))))\\\\=P(-0.5<z<1)\ \ [\because z=(x-\mu)/((\sigma)/(√(n)))]\\\\=P(z<1)-P(z<-0.5)\\\\=P(z<1)-(1-P(z<0.5))\ \ [\because\ P(Z<-z)=1-P(Z<z)]\\\\=0.8413-(1-0.6915)\ \ [\text{By z-table}]\\\\=0.5328`

b) Total resistors = 25

Let Z be the total resistance of 25 resistors.

To find P(Z≤5100 ohms) , first we find the mean and variance for Z.

Mean= E(Y) = E(25 X)=25 E(X)=25(200)= 5000 ohm

`Var(Y)=Var(25\ X)=25^2((\sigma^2)/(n))=25^2((10)^2)/(25)=2500`

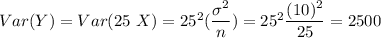
The probability that the total resistance does not exceed 5100 ohms will be :

`P(Y\leq5000)=P((Y-\mu)/(√(Var(Y)))<(5100-5000)/(√(2500)))\\\\=P(z\leq2)=0.9772\ \ [\text{By z-table}]`

Hence, the probability that the total resistance does not exceed 5100 ohms = 0.9772