Answer:
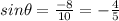
Explanation:
For this case we have a point given (-6,-8) and we know that this point is terminal side of 0
We can assume that the length of th opposite side is given by:
b=-8 and the length for the adjacent side would be a=-6
And we can find the hypothenuse on this way:
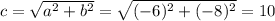
From the definition of sin we know this:
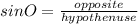
And if we replace we got this:
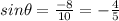
We can aslo find the cos with the following identity:
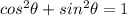
And then:

But since both corrdinates are negative we are on the 3 quadrant and then
