Question

What is the radian measure of the central angle of a circle of radius 1.5 meter that intercepts an arc of length 600 centimeters

Answer 1

Radian measure of the central angle is 4 radian

Solution:

Given that,

A circle of radius 1.5 meter that intercepts an arc of length 600 centimeters

To find: Radian measure of the central angle

Let us find the circumference of circle

The circumference of circle is given as:

`\text{ circumference of circle } = 2 \pi r`

Where "r" is the radius of circle

`\text{ circumference of circle } = 2 * \pi * 1.5 = 3 \pi`

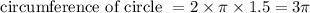
Therefore circumference of circle =
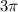`3 \pi` meters , which subtends central angle of
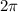`2 \pi` radian

Given that arc of length 600 centimeters. Let us convert 600 centimeter to meter

We know that, to convert centimeter to meter divide the length value by 100

`\text{ 600 centimeter } = (600)/(100) \text{ meter } = 6 \text{ meter}`

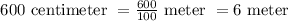
Therefore arc of 6 meter will subtend a central angle of:

`\rightarrow (6)/(3 \pi) * 2 \pi = 4`

Therefore radian measure of the central angle is 4 radian