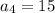Answer:
The value of
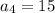
Explanation:
Given that
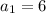 and
and
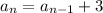
Given sequence is of the form arithmetic sequence
For arithmetic sequence the sequence is
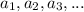
The nth term is of the form

Here
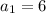 and
and
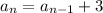
from this the common differnce is 3.
Therefore d=3
To find
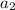 ,
,
 ,
,
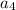

put n=2 and d=3 we get
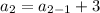
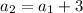
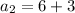 (here
(here
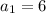 )
)
Therefore


put n=3 and d=3 we get
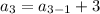
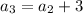
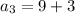 (here
(here
 )
)
Therefore


put n=4 and d=3 we get
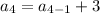
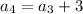
 (here
(here
 )
)
Therefore
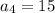
Therefore the sequence is 6,9,12,15,...
Therefore the value of