Question

Drag each number to the correct location on the table. Each number can be used more than once, but not all numbers will be used.

Simplify the given polynomial expressions, and determine the degree and number of terms in each expression.
Degree
Degree
Number of
Terms
4x + 2.2(3x - 5)
(-304 +503 - 12) + (7x3 - 25 + 6)
(3x2 – 3)(3x2 + 3)

Answer 1

1.
`12x^2-13.4x-11`

- Degree: 2

- Number of terms: 3

2.
`7x^3+168`

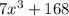
- Degree: 3

- Number of terms: 2

3.
`9x^4-9`

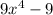
- Degree: 4

- Number of terms: 2

Step-by-step explanation:

For this exercise you need to remember the multiplication of signs:

`(+)(+)=+\\(-)(-)=+\\(-)(+)=-\\(+)(-)=-`

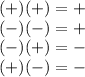
1. Given:

`(4x + 2.2)(3x - 5)`

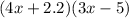
Apply the Distributive property:

`=12x^2+6.6x-20x-11`

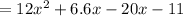
Add the like terms:

`=12x^2-13.4x-11`

You can idenfity that:

- Degree: 2

- Number of terms: 3

2. Given:

`(-304 +503 - 12) + (7x^3 - 25 + 6)`

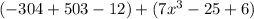
Add the like terms:

`=187 + 7x^3 - 25 + 6=7x^3+168`

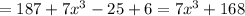
You can idenfity that:

- Degree: 3

- Number of terms: 2

3. Given:

`(3x^2 - 3)(3x^2 + 3)`

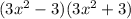
Apply Distributive property:

`=9x^4-9x^2+9x^2-9`

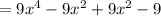
Add the like terms:

`=9x^4-9`

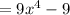
You can idenfity that:

- Degree: 4

- Number of terms: 2