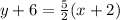Question

The table represents a linear equation. A two column table with 5 rows. The first column, x, has the entries, negative 4, negative 2, 6, 10. The second column, y, has the entries, negative 11, negative 6, 14, 24. Which equation correctly uses point (–2, –6) to write the equation of this line in point-slope form? y – 6 = y minus 6 equals StartFraction 5 Over 2 EndFraction left-parenthesis x minus 2 right parenthesis.(x – 2) y – 6 = negative StartFraction 2 Over 5 EndFraction. (x – 2) y + 6 = y plus 6 equals StartFraction 2 Over 5 EndFraction left-parenthesis x plus 2 right parenthesis.(x + 2) y + 6 = y plus 6 equals StartFraction 5 Over 2 EndFraction left-parenthesis x plus 2 right parenthesis.(x + 2)

Answer 1

`y+6=(5)/(2)(x+2)`

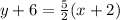
y plus 6 equals StartFraction 5 Over 2 EndFraction left-parenthesis x plus 2 right parenthesis.

Explanation:

we have the ordered pairs

`(-4,-11),(-2,-6),(6,14),(10,24)`

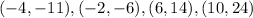
step 1

Find the slope

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

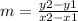
take the points

`(-4,-11),(-2,-6)`

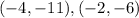
substitute the given values

`m=(-6+11)/(-2+4)`

`m=(5)/(2)`

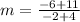
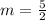
step 2

Find the equation in point slope form

`y-y1=m(x-x1)`

we have

`m=(5)/(2)`

`(x1,y1)=(-2,-6)`

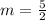
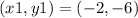
substitute in the equation

`y-(-6)=(5)/(2)(x-(-2))`

`y+6=(5)/(2)(x+2)`