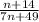Question

Two fire hoses are used to extinguish a fire. Hose A, when turned on alone, can extinguish the fire in 7 minutes, while hose B takes "n" minutes more time than hose A. Find an expression (in terms of "n") for how much of the fire they will extinguish in 1 minute when both hoses are turned on together.

Answer 1

The expression in terms of "n" for how much of the fire they will extinguish in 1 minute when both hoses are turned on together is
`(n + 14)/(7n + 49)`

Solution:

Given that,

Hose A, when turned on alone, can extinguish the fire in 7 minutes

Hose B takes "n" minutes more time than hose A

Hose takes (n + 7) minutes to extinguish the fire

STEP 1: Calculate how much work (here work is to extinguish the fire) each person does in one minute

`Hose A = (1)/(7)th \text{ of the work }\\\\Hose B = (1)/(n+7)th \text{ of the work }`

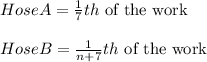
STEP 2: Add up the amount of work done by each person in one minute

Work done in one minute when both are working together:

`\rightarrow (1)/(7) + (1)/(n + 7)\\\\\rightarrow (n + 7 + 7)/(7n + 49)\\\\\rightarrow (n + 14)/(7n + 49)`

Therefore, the expression in terms of "n" for how much of the fire they will extinguish in 1 minute when both hoses are turned on together is:

`(n + 14)/(7n + 49)`