2 Answers

Ohblahitsme · Answer 1 · 2021-06-23T01:22:34+0000

The solutions for ‘x’ in the given equation are – 3 and - 7

Explanation:

Given equation:

x^(2) + 10 x + 21 = 0

To find the ‘x’ value, try to factor, because in this case it works, it's fast. By using factor method, we get

(x + 3) (x + 7) = 0 (adding both value we get 10 and multiply as 21 as in equation and check with signs also while factoring)

x = - 3, -7

Verify above values by multiply both terms,

(x + 3) (x + 7) = 0

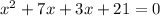
x^(2) + 7 x + 3 x + 21 = 0

x^(2) + 10 x + 21 = 0 (so values obtained from factor method are correct)

Or, can use quadratic formula, for
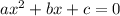a x^(2) + b x + c=0 , the solutions are given by:

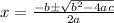
$x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}$

In the given equation, a = 1, b = 10, c = 21, apply these in above formula

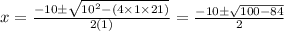
$x=\frac{-10 \pm \sqrt{10^(2)-(4 * 1 * 21)}}{2(1)}=(-10 \pm √(100-84))/(2)$

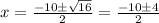
$x=(-10 \pm √(16))/(2)=(-10 \pm 4)/(2)$

So,

When
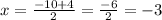
x=(-10+4)/(2)=(-6)/(2)=-3

When
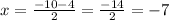
x=(-10-4)/(2)=(-14)/(2)=-7

Hence, the values for ‘x’ are - 3 and - 7

Please log in or register to add a comment.