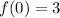Answer:
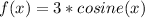
Explanation:
We are looking for a trigonometric function which contains the point (0, 3), and has an amplitude of 3.
We know that for a sine function
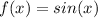 ,
,
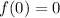 ; therefore the function we a looking for cannot be a sine function because it is zero at
; therefore the function we a looking for cannot be a sine function because it is zero at
 .
.
However, the cosine function
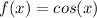 gives non-zero value at
gives non-zero value at
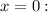
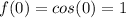
therefore, a cosine function can be our function.
Now, cosine function with amplitude
 has the form
has the form
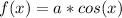
this is because the cosine function is maximum at
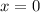 and therefore, has the property that
and therefore, has the property that
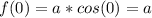
in other words it contains the point
 .
.
The function we are looking for contains the point
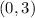 ; therefore, its amplitude must be 3, or
; therefore, its amplitude must be 3, or

we see that this function satisfies our conditions:
 has amplitude of 3, and it passes through the point (0, 3) because
has amplitude of 3, and it passes through the point (0, 3) because