Question

A Chemist needs to mix a 20% acid solution with a 50% acid solution to obtain 15 liters of a 34% acid solution. How many liters of each acid solution must be used?

Please explain well!!

Answer 1

8 Liters of 20% acid and 7 Liters of 50% acid

Explanation:

Let we mix "x" liters of 20% acid, and

"y" liters of 50% acid

Total is 15 liters, so we can write:

x + y = 15

or x = 15 - y

Then,

We mix x liters of 20% (20/100=0.2) and y liters of 50% (50/100=0.5) acid solution to make 15 liters of 34% (34/100=0.34) solution, we can write:

0.2x + 0.5y = 0.34(15)

This becomes:

`0.2x + 0.5y = 5.1`

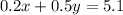
We replace x with what we got in 1st equation and solve for y:

`0.2x + 0.5y = 5.1\\0.2(15-y) + 0.5y = 5.1\\3-0.2y+0.5y=5.1\\0.3y=5.1-3\\0.3y=2.1\\y=(2.1)/(0.3)\\y=7`

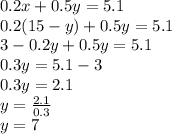
We know x = 15 - y, so

x = 15 - 7

x = 8

So, we use 8 Liters of 20% acid and 7 Liters of 50% acid