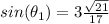Question

15'

The angle 01 is located in Quadrant I, and cos(01) = = .
What is the value of sin(01)?
Express your answer exactly.
sin(01) =(

Answer 1

`sin(\theta_1)=3(√(21))/(17)`

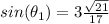
Explanation:

The complete question is

The angle θ1 is located in Quadrant 1, and cos (θ1)=10/17.

What is the value of sin(θ1)?

we know that

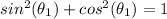`sin^2(\theta_1)+cos^2(\theta_1)=1` ---> trigonometric identity

we have

`cos(\theta_1)=(10)/(17)`

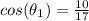
The angle
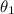`\theta_1` is located in Quadrant I, that means the sine of angle
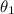`\theta_1` is positive

substitute the given value in the trigonometric identity

`sin^2(\theta_1)+((10)/(17))^2=1`

`sin^2(\theta_1)+(100)/(289)=1`

`sin^2(\theta_1)=1-(100)/(289)`

`sin^2(\theta_1)=(189)/(289)`

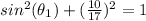
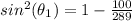
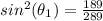
take square root both sides

`sin(\theta_1)=\pm(√(189))/(17)`

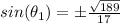
Remember that the sine is positive (Quadrant I)

so

`sin(\theta_1)=(√(189))/(17)`

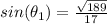
Simplify

`sin(\theta_1)=3(√(21))/(17)`