Answer:
0 ≤ t ≤ 5.
Explanation:
In the function
,
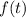is the independent variable. The domain of
is the set of all values of
that this function can accept.
In this case,
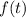is defined in a real-life context. Hence, consider the real-life constraints on the two variables. Both time and volume should be non-negative. In other words,
.
.
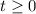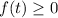The first condition is an inequality about
, which is indeed the independent variable.
However, the second condition is about
, the dependent variable of this function. It has to be rewritten as a condition about
.
![\begin{aligned} f(t) &\ge 0 &&\text{Assumption} \cr 80000 - 16000\, t& \ge 0 && \text{Definition of} ~ f \cr 80000 & \ge 16000\, t && \begin{aligned}&\text{Add $16000\, t$} \\[-0.5em] & \text{to both sides of the inequality}\end{aligned} \cr 5 &\ge t &&\begin{aligned}&\text{Divide both sides of} \\[-0.5em] & \text{the inequality by $16000$}\end{aligned} \cr t &\le 5 && \text{Flip the inequality}\end{aligned}]()
.
Hence, t ≤ 5.
Combine the two inequalities to obtain the domain:
0 ≤ t ≤ 5.