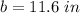Question

Use the information to answer the questions.

In triangle ABC, a = 11 in., measure angle B=70 deg and

c = 9 in.

Which information about the triangle is given?

Answer 1

Part 1) The length of two sides and the measure of the included angle (Side-Angle-Side)

Part 2)
`b^2=a^2+c^2-2(a)(c)cos(B)`

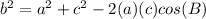
Part 3)
`b=11.6\ in`

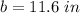
Explanation:

we have

In the triangle ABC

`a=11\ in\\c=9\ in\\B=70^o`

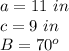
Part 1) Which information about the triangle is given?

In this problem we have the length of two sides and the measure of the included angle (Side-Angle-Side)

see the attached figure to better understand the problem

Part 2) Which formula can you use ti find b?

I can use the law of cosines

`b^2=a^2+c^2-2(a)(c)cos(B)`

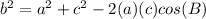
we have

`a=11\ in\\c=9\ in\\B=70^o`

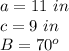
substitute the given values

`b^2=11^2+9^2-2(11)(9)cos(70^o)`

`b^2=202-67.72`

`b=11.59\ in`

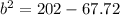
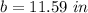
Part 3) What is b, rounded to the nearest tenth?

Remember that

To Round a number

a) Decide which is the last digit to keep

b) Leave it the same if the next digit is less than
`5` (this is called rounding down)

c) But increase it by
`1` if the next digit is
`5` or more (this is called rounding up)

In this problem we have

`11.59\ in`

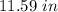
We want to keep the digit
`5`

The next digit is
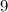`9` which is 5 or more, so increase the "5" by 1 to "6"

therefore

`b=11.6\ in`