Question

Mathematics MH helpo

Answer 1

Answer: -5x - 10 > 5

Explanation:

Answer 2

The inequalities that require flipping the sign are:

-5x - 10 > 5

`(x)/(-7) + 3 \leq 4`

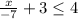
Solution:

Let us the inequalities one by one

You can perform on operations on both sides of inequality, and have its truth value unchanged

But if we multiply or divide by a negative number , we must flip the sign

option 1)

-5x - 10 > 5

Move -10 from L.H.S to R.H.S

-5x > 5 + 10

-5x > 15

Divide the above expression by 5

`-x > 3`

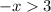
Divide the above inequality by -1, so we must flip the sign

x < -3

option 2)

`7x - 5 \leq 16`

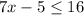
Move the constant term from L.H.S to R.H.S

`7x \leq 16 + 5\\\\7x \leq 21\\\\`

Divide the above inequality by 7

`x \leq 3`

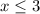
This does not required flipping the symbol

option 3

`(x)/(5) - 6 > -11`

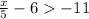
Move the constant term from L.H.S to R.H.S

`(x)/(5) > -11 + 6\\\\(x)/(5) > -5`

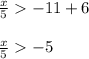
Multiply both the sides by 5

`x > -25`

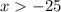
This does not required flipping the symbol

option 4

`x + 12 \leq 29`

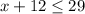
Move the constant term from L.H.S to R.H.S

`x \leq 29 - 12\\\\x \leq 17`

This does not required flipping the symbol

option 5

`(x)/(-7) + 3 \leq 4`

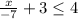
Move the constant term from L.H.S to R.H.S

`(x)/(-7) \leq 4-3\\\\(x)/(-7) \leq 1\\\\`

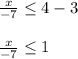
Multiply both the sides by -7, so we must flip the sign

`x \geq -7`

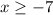
Thus this requires flipping the sign