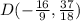Answer:
Explanation:
If CD is a diameter of circle S, then CD goes through circle S at point S. CS is a radius, and so is DS. That means that they are the same length. That also means that S is the midpoint of CD. We can use the midpoint formula and the 2 points we are given to find the other endpoint, D.
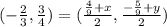
To solve for x, we will use the x coordinate of the midpoint; likewise for y. x first:
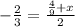
Multiply both sides by 2 to get rid of the lowermost 2 and get

Subtract 4/9 from both sides to get
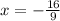
Now y:
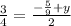
Again multiply both sides by that lower 2 to get
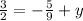
Add 5/9 to both sides to get
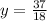
And there you go!