Answer:
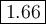
Explanation:
1. Calculate the equation of the straight line joining A and C.
The equation for a straight line is
y = mx + b
where m is the slope of the line and b is the y-intercept.
The line passes through the points (-½, 4) and (1, ⅔)
(a) Calculate the slope of the line
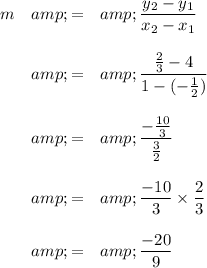
(b) Find the y-intercept
Insert the coordinates of one of the points into the equation
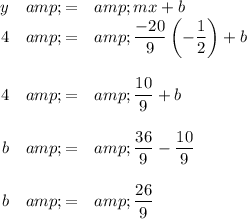
(c) Write the equation for the line
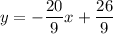
2. Calculate the value of x when y = -⅘

The graph below shows your three collinear points.