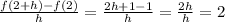Answer:
Explanation:
This kinda looks like the limiting definition of a derivative.
Anyway, what we are doing with the f(2 + h) is evaluating f(x) with 2+h in place for x. That looks like this:
f(2 + h) = 2(2 + h) - 3 which simplifies to
f(2 + h) = 4 + 2h - 3 which simplifies to
2h + 1
From that we are subtracting f(2). What we are doing with that is evaluating f(x) with 2 in place for x. That looks like this:
f(2) = 2(2) - 3 which simplifies to
f(2) = 4 - 3 which simplifies to
f(2) = 1. Now put those together over h to get: