Answer:
968 ways
Explanation:
This is a question of permutation and combination.
Each equation can have two different answers.
Thus the total number of cases will be (for 10 questions) :
 cases.
cases.
Now to find the number of ways to at least answer 3 questions False will be total minus the number of question with at most 2 False answers.
- Number of ways in which no answer is False : 1 ( all are true )
- Number of ways in which ONLY one answer is False :
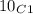 where
where
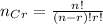
- Number of ways in which ONLY two answers are False :
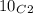
Total ways (at most 2 answers false) =
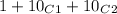 ;
;
∴
The number of ways in which at least 3 have False as the answer is :
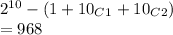 WAYS.
WAYS.