Question

Suppose that normal human body temperatures are normally distributed with a mean

of 37°C and a standard deviation of 0.2°C.
What percent of humans have a temperature between 36.6°c and 37.4°c?
Which normal curve is shaded correctly for this problem?

Answer 1

Answer: Choice B

Step-by-step explanation:

Let's convert the raw score x = 36.6 to its corresponding z score.

z = (x-mu)/sigma

z = (36.6 - 37)/(0.2)

z = -2

Note that mu and sigma represent the mean and standard deviation respectively. The score z = -2 means we're 2 standard deviations below the mean.

Following those similar steps, you should find that x = 37.4 leads to z = 2.

The temperatures we're focused are on the interval
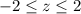`-2 \le z \le 2`, i.e. the z values are between -2 and 2 inclusive.

Therefore, the range of temperatures are within 2 standard deviations of the mean.

Visually, we'll go for choice B since this shows the lower two sections shaded (ie the panels to the left of the center) and also the upper two sections shaded. According to the Empirical Rule, this accounts for roughly 95% of the normal distribution.