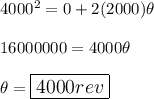Hi there!
Begin by solving for the angular acceleration using the following:

ωf = final angular velocity (4000 rpm)
ωi = initial angular velocity (0 rpm)
α = angular acceleration (r/m²)
t = time (min)
Solve:
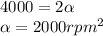
Now, we can use the rotational kinematic equation:
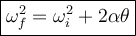
Plug in the known values: