the total surface area of the solid object is
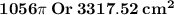
Answer:
Solution given:
diameter [d]=12 cm
radius [r]=
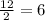 cm
cm
height of cylinder[H]=80cm
slant height [L]=10cm
Now,
Surface Area of cylinder=
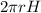
=

Surface Area of Cone:
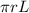
=
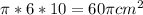
Surface area Base of solid=
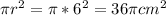
The total surface area of the object:
=Surface Area of cylinder + Surface Area of Cone+ Surface area Base of solid
=
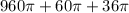
=
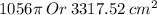
Explanation: