Question 4:
2x + 3y = 17 -- equation 1
5x + 6y = 32 -- equation 2
(equation 1) * 2
4x + 6y = 34 -- equation 3
(equation 2) - (equation 3)
x = -2 -- equation 4
plug (equation 4)'s value of x into (equation 1)
2(-2) + 3y = 17
3y - 4 = 17
3y = 21
y = 7
Thus the answer is x = -2 and y = 7
Question 5:
The vertex form of a quadrilateral looks like this:
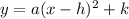
- a : coefficient of
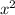
- (h,k): coordinate of the vertex.
The x-coordinate of the vertex is equal to '-b/2a'. Where b is the
coefficient of x, so:
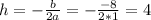
There is also another formula to find the y-value of the vertex
coordinate, but the easier way to find it is to plug it into the original
equation:

Since we know now that h = 4 and k = -4 and that a = 1, lets plug it into
the original equation.

Thus the answer is
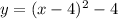
Hope that helps!