- Explanation:
How to transform a repeating decimal into a fraction?
To convert a decimal into a fraction we would usuallly write it over 100 and if it can be simplified any further we would. On the other hand repeating decimals are a bit different.
Let‘s see how to convert them:
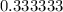
Imagine this decimal goes on and on forever and I want to convert it into a
fraction:
1. First step is to multiply by a factor of 10 then misusing it by a factor of one which would give you a whole number.
So let’s say:
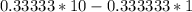
- It’s because the digits match up to subtract to a whole number so if I find the value is would be 3/9 since 10 - 1 is equal to 9 and 3.3333 - 0.33333 would be 3 but I can simplify this to 1/3.
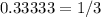
Now let’s use this knowledge to calculat a value:

Let’s convert this repeating decimal into a fraction:
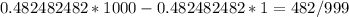
I have multiplied it by 1000 because that’s when we minus it gives me a whole number: 482.
Okay know let’s add them together:
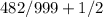
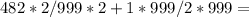
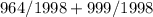
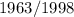
So the answer to 1/2 + the repeating decimal(0.482482) is 1963/1998
If you would like to learn further:
Watch: Converting Repeating Decimal to Fraction on Khan Academy
Note: I can’t paste the link because it says it contains swear words!