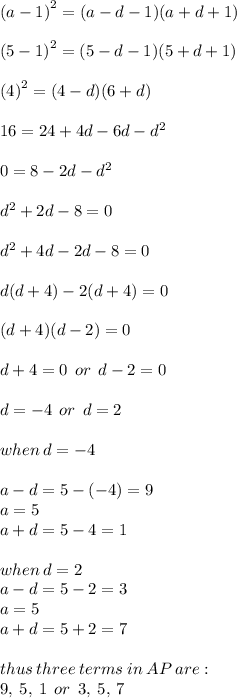Question

The sum of three terms in AP is 15. If the first two terms are each decreased by 1 and the last is increased by 1 then the resulting terms are in GP. find the numbers.​

Answer 1

3, 5, ,7 or 9, 5, 1

Explanation:

Let the three terms in AP be a - d, a & a + d

where a = First term and d = Common difference.

Condition 1: sum of three terms in AP is 15.

a - d + a + a + d = 15

3a = 15

a = 15/3

a = 5

Condition 2: When first two terms are each decreased by 1 and the last is increased by 1 then new terms so obtained will be as follows:

a - d - 1, a - 1, a + d + 1

These terms are in G.P.

`{(a - 1)}^(2) = (a - d - 1)(a + d + 1) \\ \\ {(5 - 1)}^(2) = (5 - d - 1)(5 + d + 1) \\ \\ {(4)}^(2) = (4 - d)(6 + d) \\ \\ 16 = 24 + 4d - 6d - {d}^(2) \\ \\ 0 = 8 - 2d - {d}^(2) \\ \\ {d}^(2) + 2d - 8 = 0 \\ \\ {d}^(2) + 4d - 2d - 8 = 0 \\ \\ d(d + 4) - 2(d + 4) = 0 \\ \\ (d + 4)(d - 2) = 0 \\ \\ d + 4 = 0 \: \: or \: \: d - 2 = 0 \\ \\ d = - 4 \: \: or \: \: d = 2 \\ \\ when \: d = - 4 \\ \\ a - d = 5 - ( - 4) = 9 \\ a = 5 \\ a + d = 5 - 4 = 1 \\ \\ when \: d = 2 \\ a - d = 5 - 2 = 3 \\ a = 5 \\ a + d = 5 + 2 = 7 \\ \\ thus \: three \: terms \: in \: AP \: are: \\9, \: 5, \: 1 \: \: or \: \: 3, \: 5, \: 7`