Question

= table shows a hot air balloon's height h, in feet, during a descent at various times t, in seconds.

Time Height
(seconds) (feet)
5
1150
10
1090
15
1030
20
970
25
910
at air balloon's initial rate of change (slope).

Answer 1

A. Slope is -12 feet per second

B. Yes, it is constant.

Skills needed: Linear Equations, Substitution and Division

Explanation:

1) Solving Part A (we need to find the slope):

• The slope is
  `(y_2-y_1)/(x_2-x_1)` -->
  `y_1`,
  `y_2`,
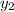  `x_1`, and
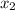  `x_2` are all values from the table. We know that the left column is the x-values, and the right column is the y-values as that is the conventional way of depicting them.

2) Using the y-values of 1150 and 1090, and their corresponding x-values (5 and 10 respectively), we can get the slope:

-
`(y_2-y_1)/(x_2-x_1)` ==>
`(1090-1150)/(10-5)` ==>
`1090-1150=-60, 10-5=5` ==>
`(-60)/(5)`

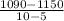`(-60)/(5) =-12`, so the slope is -12.

==================================================================

1) Part B (analysis)

We can see that no matter what 2 y-values and their corresponding x values we use, the slope always is the same. This means that the rate of change is constant.