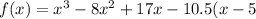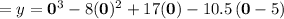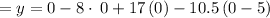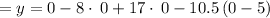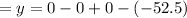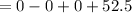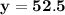Answer:
x-intercept(s): (−1.9900717, 0)
y-intercept(s): (0, 52.5)
Explanation:
To find the x-intercept, substitute in
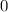 for
for
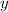 and solve for
and solve for
 . To find the y-intercept, substitute in
. To find the y-intercept, substitute in
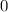 for
for
 and solve for
and solve for
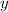 .
.
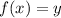
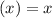
x-intercept
To find the x-intercept(s), substitute in
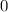 for
for
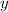 and solve for
and solve for
 .
.
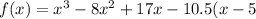
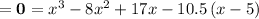
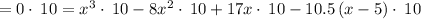
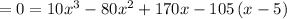
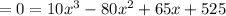
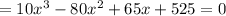
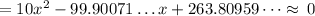
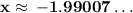
y-intercept