Question

The Haber process can be used to produce ammonia (NH3) from hydrogen gas (H2) and nitrogen gas (N2). The balanced equation for this process is shown below. 3H2 N2 Right arrow. 2NH3 The molar mass of NH3 is 17. 03 g/mol. The molar mass of H2 is 2. 0158 g/mol. In a particular reaction, 0. 575 g of NH3 forms. What is the mass, in grams, of H2 that must have reacted, to the correct number of significant figures? 0. 1 0. 102 0. 10209 0. 1021.

Answer 1

B

Step-by-step explanation:

We are given that ammonia can be produced from hydrogen gas and nitrogen gas according to the equation:

`\displaystyle 3\text{H$_2$} + \text{N$_2$} \longrightarrow 2\text{NH$_3$}`

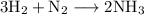
We want to determine the mass of hydrogen gas that must have reacted if 0.575 g of NH₃ was produced.

To do so, we can convert from grams of NH₃ to moles of NH₃, moles of NH₃ to moles of H₂, and moles of H₂ to grams of H₂.

We are given that the molar masses of NH₃ and H₂ are 17.03 g/mol and 2.0158 g/mol, respectively.

From the equation, we can see that two moles of NH₃ is produced from every three moles of H₂.

With the initial value, perform dimensional analysis:

`\displaystyle \begin{aligned} 0.575\text{ g NH$_3$}& \cdot \frac{1\text{ mol NH$_3$}}{17.03\text{ g NH$_3$}} \cdot\frac{3\text{ mol H$_2$}}{2\text{ mol NH$_3$}} \cdot \frac{2.0158\text{ g H$_2$}}{1\text{ mol H$_2$}} \\ \\ & = 0.102\text{ g H$_2$}\end{aligned}`

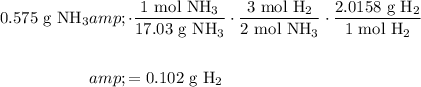
*Assuming 100% efficiency.

Our final answer should have three significant figures. (The first term has three, the second term has four (the one is exact), the third term is exact, and the fourth term has five. Hence, the product should have only three.)

In conclusion, our answer is B.