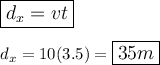Question

A ball is kicked horizontally from a 60 meter tall cliff at 10 m/s. How far from

the base of the cliff does it land?

Answer 1

Hi there!

We can begin by deriving the equation for how long the ball takes to reach the bottom of the cliff.

`\large\boxed{\Delta d = v_it+ (1)/(2)at^2}}`

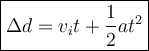
There is NO initial vertical velocity, so:

`\large\boxed{\Delta d= (1)/(2)at^2}}`

Rearrange to solve for time:

`2\Delta d = at^2\\\\t = \sqrt{(2\Delta d)/(g)}`

Plug in the given height and acceleration due to gravity (g ≈ 9.8 m/s²)

`t = \sqrt{(2(60))/((9.8))} = 3.5 s`

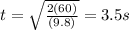
Now, use the following for finding the HORIZONTAL distance using its horizontal velocity:

`\large\boxed{d_x = vt}\\\\d_x = 10(3.5) = \karge\boxed{35 m}`