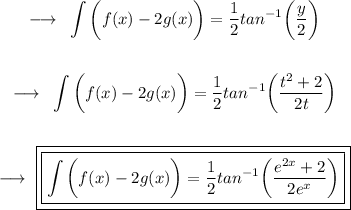Given that.
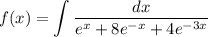
and,
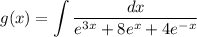
To perform mathematical operations on f(x) and g(x), they should have the same denominator.
Multiplying & Dividing f(x) by e^2x,
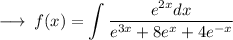
Now,
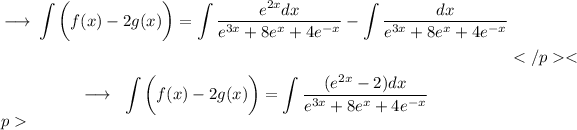
Multiplying & Dividing by e^x,
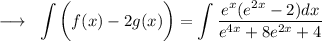
Let's assume t = e^x
Differentiating on both sides w.r.t x,
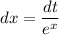
Thus,
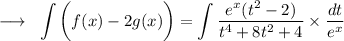
Dividing Numerator and Denominator by t²,
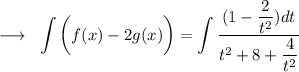
Consider t² + 8 + 4/t².
It can be rewritten as (t + 2/t)² + 4 = (t + 2/t)² + 2
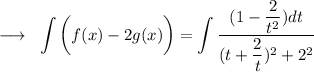
Here,
If y = t + 2/t and differentiating w.r.t t,
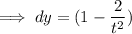
Therefore,
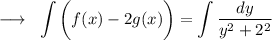
Of the form,
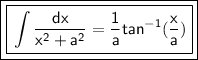
Further,