Question

The surface area of a box is 160 square inches. The length of the box is twice its width, and is 4 inches less than its height. What is the height of the box, in inches?

Answer 1

the height of the box is 9 inches

Answer:

solution given:

total surface area of a box=160 square inches

let length, width, and height be l,b, and h respectively.

according to the question:

l=2b

∴b =
`(l)/(2)`

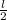
l=h-4

∴ h=l+4

we have

total surface area of a box=160 square inches

2(lb+lh+bh)=160

`2(l*(l)/(2)+l(l+4)+(l)/(2)*(l+4))=160`

`2*(l^2+2l^2+8l+l^2+4l)/(2)=160`

`4l^2+12l=160`

`4(l^2+3l)=160`

`l^2+3l=(160)/(4)`

`l^2+3l-40=0`

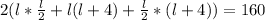
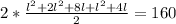
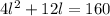
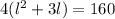
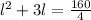
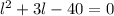
doing middle term factorization

`l^2+(8-5}l-40=0`

`l^2+8l-5l-40=0`

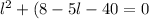
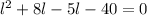
taking common from each two terms

l(l+8)-5(l+8)=0

(l+8)(l-5)=0

either

l=-8[neglected as length is always positive]

or

l=5

now

b=
`(5)/(2) =2.5`

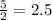
h=5+4=9

Explanation: