Assuming both billiard balls have the same mass, conservation of momentum says

where m = mass of both billiard balls, and v₁ and v₂ = their initial velocities, and v₁' and v₂' = their final velocities. The masses are the same so the exact value of m is irrelevant. The first ball has initial speed 5 m/s and the second is at rest, so

After the collision, the first ball has speed 4.35 m/s and is moving at angle of 30° below the original path, so
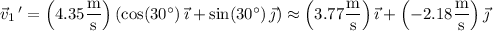
Then the second ball has final velocity vector

so it moves with speed
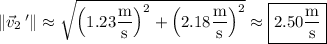
at an angle of
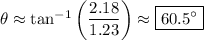
or about 60.5° above the original line of motion.