Answer:
Step-by-step explanation:
Consider the general chemical reaction
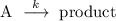 .
.
If [A] is the concentration of A (reactant) at any time t and n is the reaction order for the whole equation, the rate is then related to the concentration of reactant A with the following differential form of equation
![Rate \ = \ -\displaystyle\frac{d[\mathrm{A}]}{dt} \ = \ k[\mathrm{A}]^(n)](https://img.qammunity.org/2022/formulas/chemistry/college/7jebtk02veqdzpgbs4xuokg7eb4umv9a20.png) .
.
where k is the rate constant.
*Note that the differential term
![\displaystyle\frac{d[\mathrm{A}]}{dt}](https://img.qammunity.org/2022/formulas/chemistry/college/xugc8anagdeegzm254r4o7oqv6nfdppwaz.png) has a negative sign to denote that the concentration of A is decreasing over time t.
has a negative sign to denote that the concentration of A is decreasing over time t.
Since the chemical reaction between tert-butyl bromide and water is given to be a first-order reaction, hence n = 1, and the resulting differential equation becomes
![Rate \ = \ -\displaystyle\frac{d[\mathrm{A}]}{dt} \ = \ k[\mathrm{A}]^(1) \ = \ k[\mathrm{A}]](https://img.qammunity.org/2022/formulas/chemistry/college/mvtqwbq6j9kgscsub1h50lbaxsc5uq31b3.png)
To solve this first-order linear homogenous differential equation, the method of separation of variables can be used.
![\-\hspace{1cm} \displaystyle\frac{d[\mathrm{A}]}{dt} \ = -\ k[\mathrm{A}] \\ \\ \-\hspace{0.5cm} \displaystyle\frac{1}{[\mathrm{A}]} \, d[\mathrm{A}] \ = -\ k \, dt \\ \\ \int\ {\displaystyle\frac{1}{[\mathrm{A}]} \, d[\mathrm{A}] \ = \ -\int {k} \, {dt}](https://img.qammunity.org/2022/formulas/chemistry/college/2yxu1nfhbn4wy2b0xienym0xp8yu6y2esy.png)
![\ln{[\mathrm{A}]} \ = \ -kt \ + \ C \\ \\ \-\hspace{0.45cm} $[A]$ \ = \ e^(-kt \ + \ C) \\ \\ \-\hspace{0.45cm} $[A]$ \ = \ e^(-kt)e^(C) \ \ \ \ \ \ \ \ \ (e^(a \ + \ b) \ = \ e^(a)e^(b) \ \ \ \mathrm{by \ the \ law \ of \ indices})](https://img.qammunity.org/2022/formulas/chemistry/college/bmb27grf3gqcbd5fh4vkizdi76hkuzpauq.png)
Since the term
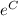 is a constant, let
is a constant, let
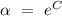 , hence
, hence
![[\mathrm{A}] \ = \ \alpha e^(-kt)](https://img.qammunity.org/2022/formulas/chemistry/college/yrg6ikcxn383ccgzjmdvxawe8qykdc9uu9.png) or
or
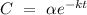 according to the question. Given that the initial concentration (t = 0) of tert-butyl bromide is 0.2 mol/L and k = 0.0537
according to the question. Given that the initial concentration (t = 0) of tert-butyl bromide is 0.2 mol/L and k = 0.0537
 , so
, so
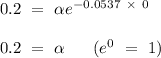
Therefore, the rate equation is
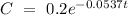 .
.
The concentration of tert-butyl alcohol after 1 hour is
