Question

A 33.4−L volume of methane gas is heated from 22°C to 66°C at constant pressure. What is the final volume of the gas?

Answer 1

38.38 L (3 d.p.)

Step-by-step explanation:

In response to questions addressing the expansion of gas via heating, Charles's Law should be considered. Charles's Law is an experimental gas law explaining the tendency of gases to expand when heated.

The law states that the volume (
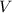`V`) of a gas is directly proportional to its temperature (
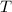`T`) given that the pressure (
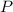`P`) and the amount of gas (
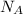`N_(A)`) are constant.

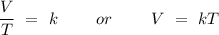`\displaystyle(V)/(T) \ = \ k \ \ \ \ \ \ \ or \ \ \ \ \ \ \ V \ = \ kT`, where k is a proportionality constant.

*Note that when substituting temperature into the equation, the temperature must be in terms of the Kelvin scale and not in degrees Celsius. The relation between the Kelvin scale and the Celsius scale is
`\mathrm{K} \ = \ ^(\circ)\mathrm{C} \ + \ 273`.

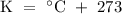Charles's law can be used to compare changing conditions of a particular gas. Let
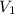`V_(1)` and
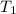`T_(1)` be the initial volume and temperature for the gas, while
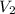`V_(2)` and
`T_(2)` be the final volume and temperature. The mathematical relationship of Charles's law becomes:

`\displaystyle(V_(1))/(T_(1)) \ = \ \displaystyle(V_(2))/(T_(2))`.

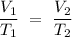In accordance with the question,

`V_(1) \ = \ 33.4 \ \mathrm{L}, \ T_(1) \ = \ (22 \ + \ 273) \ \mathrm{K} \ = \ 295 \mathrm{K}, \ T_(2) \ = \ (66 \ + \ 273) \ \mathrm{K} \ = \ 339 \ \mathrm{K}`

while
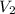`V_(2)` is the final volume of the gas that we would like to find. Therefore,

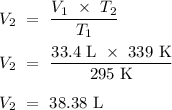`V_(2) \ = \ \displaystyle(V_(1) \ * \ T_(2))/(T_(1)) \\ \\ V_(2) \ = \ \displaystyle\frac{33.4 \ \mathrm{L} \ * \ 339 \ \mathrm{K}}{295 \ \mathrm{K}} \\ \\ V_(2) \ = \ 38.38 \ \mathrm{L}`.