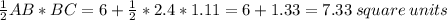Question

In the rectangular trapezoid ABCD AC is driven by a CD (see figure).

Find the width of the trapezoid if AC = 3, AD = 5.

Answer 1

solution given:

let's see only in a right-angled triangle Δ ACD.

AC=3 units

AD=5 units

since Δ ACD is a right-angled triangle. It satisfies Pythagoras law

`AD^(2)=AC^(2)+CD^(2)`

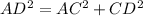
25=9+
`CD^2`

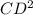
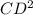`CD^2`=25-9=16

`CD=√(16) =4 units`

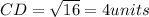
Now

Area of rectangle Δ ACD=
`(1)/(2) CD*AC=(1)/(2)*4*3=6\: square \:units`

similarly,

`(1)/(2) AD*CE=6\: square \:units\\ 5*CE=6*2\\CE=(12)/(5)=2.4 units`

since AB=CE=2.4 units

Δ ACE is a right-angled triangle. It satisfies Pythagoras law.

`AC^(2)=AE^(2)+CE^(2)\\3^2=AE^2+2.4^2\\9-5.76=AE^2\\AE and BC=√(1.24) =1.11 units`

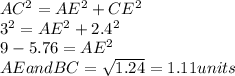
now

area of trapezoid=area ofΔACD+Area of ΔABC

=6+
`(1)/(2)AB*BC=6+(1)/(2)*2.4*1.11=6+1.33 =7.33\: square \:units`