Question

Answer the Both (a) and (b) . And show the method too. I will make Brainelist + 50 points​

Answer 1

#a

• 4p-6pq+9q-6
• 4p-3(2pq+3q-2)

#b

That be x and y

So

• x+y=15--(1)
• 2x+4y=64--(2)

So

from eq(1)

• x=15-y--(3)

Put in second one

• 2(15-y)+4y=64
• 30-2y+4y=64
• 2y=34
• y=17

Put in third one

• x=15-17
• x=-2

Take it positive

• x=2

Answer 2

(a) (i) Factorize
`\sf 4p-6pq+9q-6`

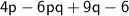
Rewrite by swapping the order of the first two terms:

⇒ -6pq + 4p + 9q - 6

Factorize the first two terms and the last two terms separately:

⇒ -2p(3q - 2) + 3(3q - 2)

Factor out the common term (3q - 2):

⇒ (3q - 2)(-2p + 3)

(ii)

Square of the binomial:
`(a+b)^2=a^2+2ab+b^2`

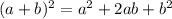
Rewrite
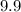`9.9` as
`10 - 0.1`

Therefore,
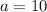`a = 10` and
`b = -0.1`

Also, remember that multiplying a number by 0.1 is the same as dividing it by 10. (when dividing a decimal number by 10, simply move the decimal point 1 place to the left).

`\begin{aligned}\implies 9.9^2 & =(10-0.1)^2\\ & =10^2-2 \cdot 10 \cdot 0.1+0.1^2\\& = 100-(2 \cdot 10)/(10)+(0.1)/(10)\\& =100-2+0.01\\ & =98 + 0.01\\ & = 98.01\end{aligned}`

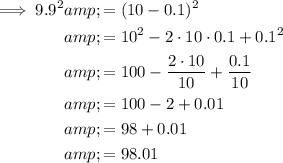
(b) (i)

Let x = number of motor bicycles

Let y = number of cars

Given:

• There are 15 vehicles of two types

⇒ x + y = 15

Given:

• The number of tires in all vehicles is 64
  - Motor bicycles have 2 tires each
  - Cars have 4 tires each

⇒ 2x + 4y = 64

(ii) Rewrite x + y = 15 to make x the subject:

⇒ x = 15 - y

Substitute into 2x + 4y = 64 and solve for y:

⇒ 2(15 - y) + 4y = 64

⇒ 30 - 2y + 4y = 64

⇒ 30 + 2y = 64

⇒ 2y = 34

⇒ y = 17 cars

Substitute found value of y into x = 15 - y to find x:

⇒ x = 15 - 17 = -2 motorbikes

**There must be an error in the question, as with the given information, the number of motorbikes is -2, which is impossible.**

Here are the possible combinations of number of motorbikes (M) and number of cars (C) whose sum of tires is 64. As you can see, there is no combination that sums to 15 vehicles:

0 M + 16 C = 16 vehicles

2 M + 15 C = 17 vehicles

4 M + 14 C = 18 vehicles

6 M + 13 C = 19 vehicles

8 M + 12 C = 20 vehicles

10 M + 11 C = 21 vehicles

12 M + 10 C = 22 vehicles

14 M + 9 C = 23 vehicles

16 M + 8 C = 24 vehicles

18 M + 7 C = 25 vehicles

20 M + 6 C = 26 vehicles

22 M + 5 C = 27 vehicles

24 M + 4 C = 28 vehicles

26 M + 3 C = 29 vehicles

28 M + 2 C = 30 vehicles

30 M + 1 C = 31 vehicles

32 M + 0 C = 32 vehicles