the length of the side of this square is
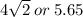 cm
cm
Answer:
Solutions Given:
let diagonal of square be AC: 8 cm
let each side be a.
As diagonal bisect square.
let it forms right angled triangle ABC .
Where diagonal AC is hypotenuse and a is their opposite side and base.
By using Pythagoras law
hypotenuse ²=opposite side²+base side²
8²=a²+a²
64=2a²
a²=

a²=32
doing square root on both side

a=±

a=±2*2

Since side of square is always positive so
a=4
 or 5.65 cm
or 5.65 cm