Answer:
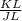 =
=
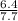 = 0.83
= 0.83
Explanation:
The key understanding here is that ΔJKL is similar to triangle 3 based on the AA criterion (they both have a right angle and a 40° angle).
We can find
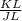 by setting up a proportion statement that includes KL, JL, and the lengths of their corresponding sides in triangle 3.
by setting up a proportion statement that includes KL, JL, and the lengths of their corresponding sides in triangle 3.
We can use this proportion:
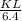 =
=
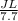
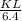 ⇒ opposite to 40° angle
⇒ opposite to 40° angle
KL, JL ⇒ ΔJKL
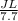 ⇒ adjacent to 40° angle
⇒ adjacent to 40° angle
6.4, 7.7 ⇒ triangle 3
[Now see the attachment]
Now we can rewrite the equation to show the ratios of the side lengths within each triangle.
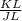 =
=
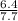
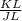 ⇒ ΔJKL
⇒ ΔJKL
KL, 6.4 ⇒ adjacent to 40° angle
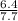 ⇒ triangle 3
⇒ triangle 3
JL, 7.7 ⇒ adjacent to 40° angle