Answer:
(a) (i) Factorize
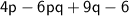
Rewrite by swapping the order of the first two terms:
⇒ -6pq + 4p + 9q - 6
Factorize the first two terms and the last two terms separately:
⇒ -2p(3q - 2) + 3(3q - 2)
Factor out the common term (3q - 2):
⇒ (3q - 2)(-2p + 3)
(ii)
Square of the binomial:
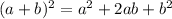
Rewrite
 as
as

Therefore,
 and
and

Also, remember that multiplying a number by 0.1 is the same as dividing it by 10. (when dividing a decimal number by 10, simply move the decimal point 1 place to the left).

(b) (i)
Let x = number of motor bicycles
Let y = number of cars
Given:
- There are 15 vehicles of two types
⇒ x + y = 15
Given:
- The number of tires in all vehicles is 64
- Motor bicycles have 2 tires each
- Cars have 4 tires each
⇒ 2x + 4y = 64
(ii) Rewrite x + y = 15 to make x the subject:
⇒ x = 15 - y
Substitute into 2x + 4y = 64 and solve for y:
⇒ 2(15 - y) + 4y = 64
⇒ 30 - 2y + 4y = 64
⇒ 30 + 2y = 64
⇒ 2y = 34
⇒ y = 17 cars
Substitute found value of y into x = 15 - y to find x:
⇒ x = 15 - 17 = -2 motorbikes
**There must be an error in the question, as with the given information, the number of motorbikes is -2, which is impossible.**
Here are the possible combinations of number of motorbikes (M) and number of cars (C) whose sum of tires is 64. As you can see, there is no combination that sums to 15 vehicles:
0 M + 16 C = 16 vehicles
2 M + 15 C = 17 vehicles
4 M + 14 C = 18 vehicles
6 M + 13 C = 19 vehicles
8 M + 12 C = 20 vehicles
10 M + 11 C = 21 vehicles
12 M + 10 C = 22 vehicles
14 M + 9 C = 23 vehicles
16 M + 8 C = 24 vehicles
18 M + 7 C = 25 vehicles
20 M + 6 C = 26 vehicles
22 M + 5 C = 27 vehicles
24 M + 4 C = 28 vehicles
26 M + 3 C = 29 vehicles
28 M + 2 C = 30 vehicles
30 M + 1 C = 31 vehicles
32 M + 0 C = 32 vehicles