Answer:
5730 years
Step-by-step explanation:
In a chemical reaction, including radioactive decay, the half-life of a species is the time taken for the substance to decrease to exactly one-half its initial value.
For a first-order reaction, the half-life of the reactant is
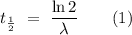 ,
,
where λ is the reaction's rate constant modeled by the differential equation describing the kinetics of a first-order reaction
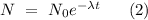 ,
,
where N is the remaining amount of substance after time t and
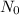 is the initial amount of substance before the chemical reaction proceeds.
is the initial amount of substance before the chemical reaction proceeds.
Since the value of λ is constant, rearrange equation (1) with λ as the subject,
 .
.
Given that only 12.5% of carbon-14 remained after 17190 years assuming that initially there was 100% of carbon -14, substitute in the values into equation (2) and solve for λ (make λ the subject of the equation),
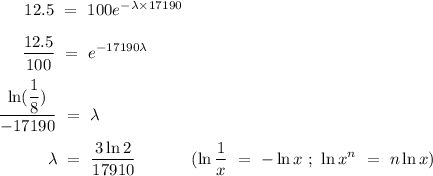
Equate both λ,
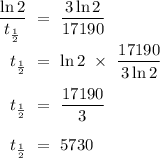
*Note that the above calculations demonstrated that carbon-14 went through 3 half-lives to yield a remaining 12.5% of its original amount, since
 .
.
Therefore, if n is the time taken for carbon-14 to half its initial amount trice to remain 12.5% of its initial amount. Then, the half-life of carbon-14 is
 .
.