Question

9) when the distance was one fourth as much, what happened to the force between the objects?

in this case (G=6.67E-11)

Answer 1

Hi there!

Recall Newton's Law of Universal Gravitation:

`\large\boxed{F_g = (Gm_1m_2)/(r^2)}`

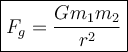
G = Gravitational Constant

m1, m2 = mass of objects (kg)

r = distance between objects (m)

There is an INVERSE-SQUARE relationship between the gravitational force and the distance between the objects, so:

`F_g = (Gm_1m_2)/(((1)/(4)r)^2) = F_g = (Gm_1m_2)/((1)/(16)r^2)`

`= 16G(m_1m_2)/(r^2) = 16F_g`

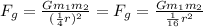
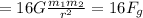
Thus, the gravitational force between the objects would INCREASE by a factor of 16.