The force
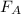 needed to stretch spring A is going to be twice as much as the force
needed to stretch spring A is going to be twice as much as the force
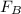 needed to stretch spring B.
needed to stretch spring B.
Step-by-step explanation:
We know that the spring constants are related as
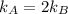
The force
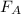 needed to stretch spring A is given by
needed to stretch spring A is given by
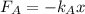
Also, the force
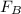 needed to stretch spring is
needed to stretch spring is
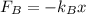
Taking the ratio of the forces, we get
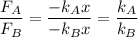
Since
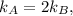 the equation above becomes
the equation above becomes
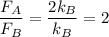
or

This shows that since the spring constant of spring A is twice as large as that of spring B, the force needed is going to be twice as large.