Question

PLEASEEEEEEE HELPPPP!

Answer 1

(3, 6)

Explanation:

1. If any factors can be cancelled out, then this indicates that there are holes in the graph.

2. To find the x-coordinate of the hole, set the factor equal to zero and solve for x.

3. Find the y-coordinate by substituting the x-coordinate back into the "reduced" function.

Here are the steps:

`f(x) = \frac{ { x }^( 2 ) -9 }{ x-3 }`

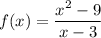
Factor the top part of the function

x² - 9

Since both terms are perfect squares, factor using the difference of squares formula, a² - b² = (a + b) (a - b) where a = x and b = 3

(x + 3) (x - 3)

Now that we have the top part of the function factored, we can solve the rest of the problem:

`f \left( x \right) = ( \left( x+3 \right) \left( x-3 \right) )/( x-3 )`

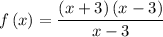
Set the factor "x - 3" equal to zero and solve for x

x - 3 = 0

Add 3 to both sides

x - 3 + 3 = 0 + 3

Simplify

x = 3

Now we need to solve for "y"

`f \left( x \right) = ( \left( x+3 \right) \left( x-3 \right) )/( x-3 )`

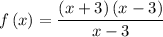
We change "f(x)", to "y"

`y = ( \left( x+3 \right) \left( x-3 \right) )/( x-3 )`

The two "x - 3" cancel out

y = x + 3

Substitute the x-value into the equation

y = 3 + 3

Add 3 and 3

y = 6

Now that we have our coordinates, we can write it as:

(x, y) = (3, 6)

So the answer is (3, 6)