Answer:

Step-by-step explanation:
We are asked to find the gravitational force between Earth and the Sun. Use the following formula:
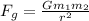
G is the universal gravitational constant. One mass (m₁) is the Earth and the other (m₂) is the Sun. r is the distance between the planets.
- G= 6.67 * 10⁻¹¹ N*m²/kg²
- m₁ = 5.97 * 10²⁴ kg
- m₂= 1.99 * 10³⁰ kg
- r= 1.48 *10¹¹ m
Substitute the values into the formula.
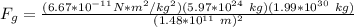
Multiply the numerator. The units of kilograms cancel.

Solve the exponent in the denominator.
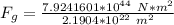
Divide. The units of meters squared cancel.
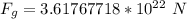
The original values all have 3 significant figures, so our answer must have the same. For the number we found, that is the hundredth place. The 7 in the thousandth place tells us to round the 1 up to a 2.
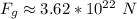
The gravitational force between Earth and the Sun is approximately 3.62 *10²² Newtons.